jz_offer_28_1.md

title	description	keywords
28. 对称的二叉树	LeetCode 28. 对称的二叉树题解，对称的二叉树，包含解题思路、复杂度分析以及完整的 JavaScript 代码实现。	LeetCode 28. 对称的二叉树 对称的二叉树 对称的二叉树 解题思路 树 深度优先搜索 广度优先搜索 二叉树

28. 对称的二叉树

🟢 Easy  🔖  树 深度优先搜索 广度优先搜索 二叉树  🔗 力扣

题目

请设计一个函数判断一棵二叉树是否 轴对称 。

示例 1：

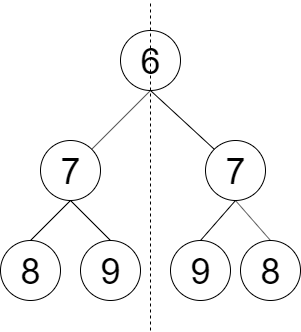
输入：root = [6,7,7,8,9,9,8]

输出：true

解释：从图中可看出树是轴对称的。

示例 2：

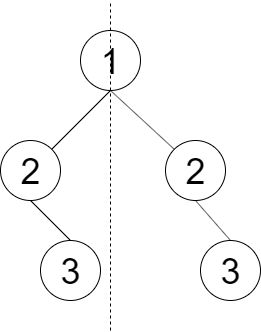
输入：root = [1,2,2,null,3,null,3]

输出：false

解释：从图中可看出最后一层的节点不对称。

提示：

• 0 <= 节点个数 <= 1000

::: warning 本题与 LeetCode 第 101 题 相同。 :::

解题思路

思路一：递归

二叉树轴对称需要满足：

• 根节点的左子节点和右子节点对称相等
• 左子节点的左子节点与右子节点的右子节点对称相等
• 左子节点的右子节点与右子节点的左子节点对称相等

递归地去判断每一层是否满足以上三个条件。

---

思路二：迭代

使用队列来对比左子树和右子树上每一个对称的节点对。

---

思路三：翻转二叉树

这道题是第 226 题 翻转二叉树 和 第 100 题 判断两颗树是否完全相等的综合题，可以将根节点的左子树翻转，然后再和根节点的右子树进行比较，是否完全相等。

代码

::: code-tabs

@tab 递归

var isSymmetric = function (root) {
	if (root == null) return true;
	const isMirror = (left, right) => {
		if (!left && !right) return true;
		if (!left || !right) return false;
		return (
			left.val == right.val &&
			isMirror(left.left, right.right) &&
			isMirror(left.right, right.left)
		);
	};
	return isMirror(root.left, root.right);
};

@tab 迭代

var isSymmetric = function (root) {
	if (!root) return true;
	let queue = [[root.left, root.right]];
	while (queue.length) {
		const [left, right] = queue.shift();
		if (!left && !right) continue;
		if (!left || !right || left.val !== right.val) return false;
		queue.push([left.left, right.right]);
		queue.push([left.right, right.left]);
	}
	return true;
};

@tab 翻转二叉树

var isSymmetric = function (root) {
	if (root == null) return true;

	// 翻转二叉树
	const invert = (root) => {
		if (root == null) return null;
		let temp = root.left;
		root.left = invert(root.right);
		root.right = invert(temp);
		return root;
	};

	// 两棵树是否全等
	const isSame = (p, q) => {
		if (p == null && q == null) return true;
		else if (p != null && q != null) {
			if (p.val != q.val) return false;
			return isSame(p.left, q.left) && isSame(p.right, q.right);
		}
		return false;
	};

	return isSame(invert(root.left), root.right);
};

:::